MySQL索引的数据结构
MySQL 索引的数据结构
二叉查找树:简单却有局限
二叉查找树(Binary Search Tree),又被称为二叉排序树,是一种基础的数据结构。它的每个节点最多包含两个子节点,分别是左子节点和右子节点 。对于树中的任意一个节点,其左子树中所有节点的值都小于该节点的值,而右子树中所有节点的值都大于该节点的值。这种特性使得二叉查找树在数据查找时具有一定的优势。
当我们要在二叉查找树中查找一个特定值时,从根节点开始,将目标值与根节点的值进行比较。如果目标值等于根节点的值,那么查找成功;如果目标值小于根节点的值,则继续在左子树中进行查找;如果目标值大于根节点的值,则在右子树中查找。重复这个过程,直到找到目标值或者遍历到叶子节点(表示查找失败)。例如,在一个包含节点值为 [3, 1, 4, 2] 的二叉查找树中查找值为 4 的节点,首先与根节点 3 比较,4 大于 3,所以在右子树中查找,右子树只有一个节点 4,查找成功。
然而,二叉查找树在面对一些情况时,查询效率会急剧下降。当数据量不断增大,并且数据插入的顺序有一定规律时,二叉查找树可能会变得非常不平衡。比如,我们按照顺序依次插入 1、2、3、4、5 这几个数字,二叉查找树会退化为一个链表结构,每个节点只有右子节点,此时树的高度等于节点数量。在这种情况下,查询时间复杂度会从理想的 O (logN) 上升到 O (N),性能大幅降低,就像在一个长长的链表中查找元素一样低效。
特点:左节点小于父节点,右节点大于父节点。
如果节点个数为n,最好的情况下,二叉查找树的查找效率为O(log n)。
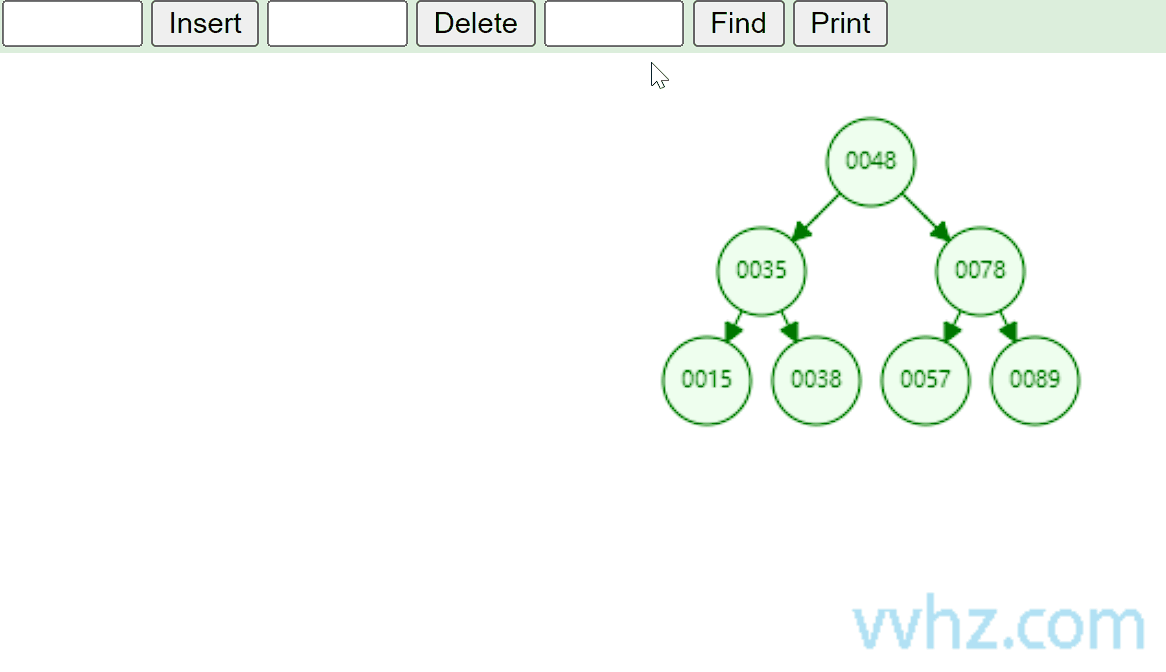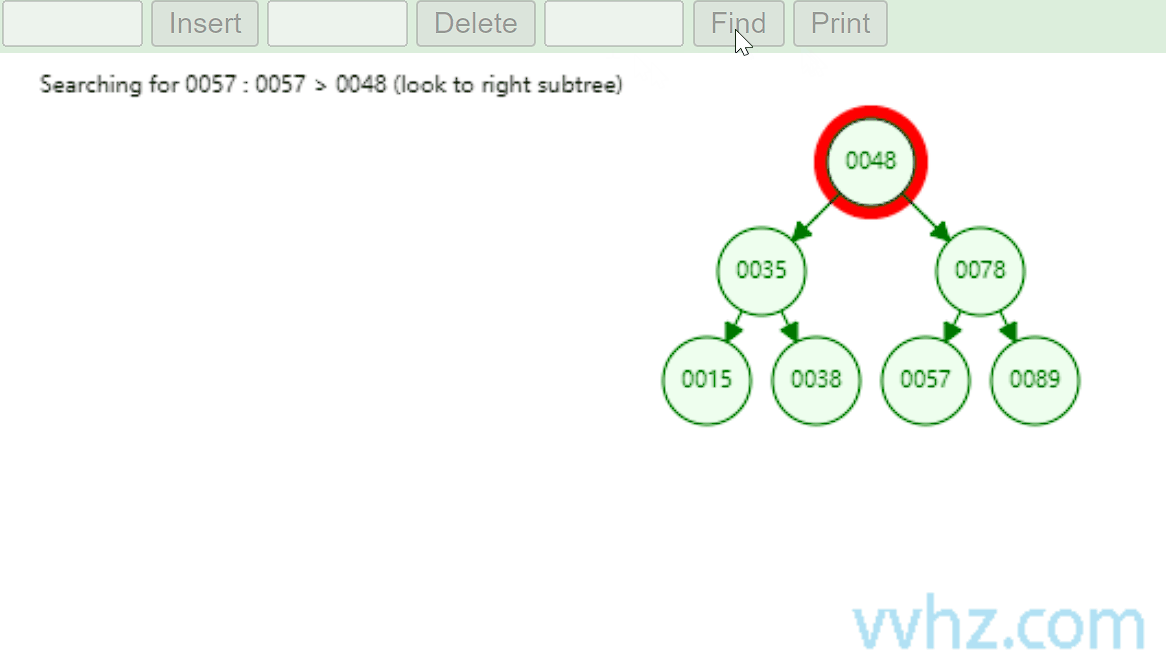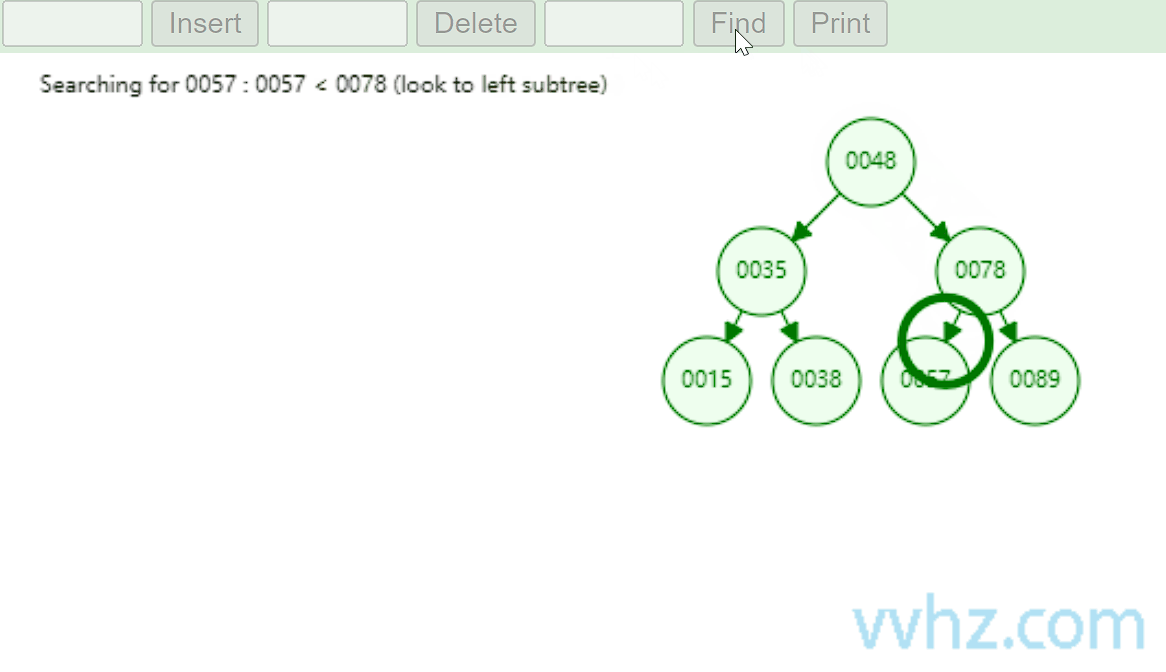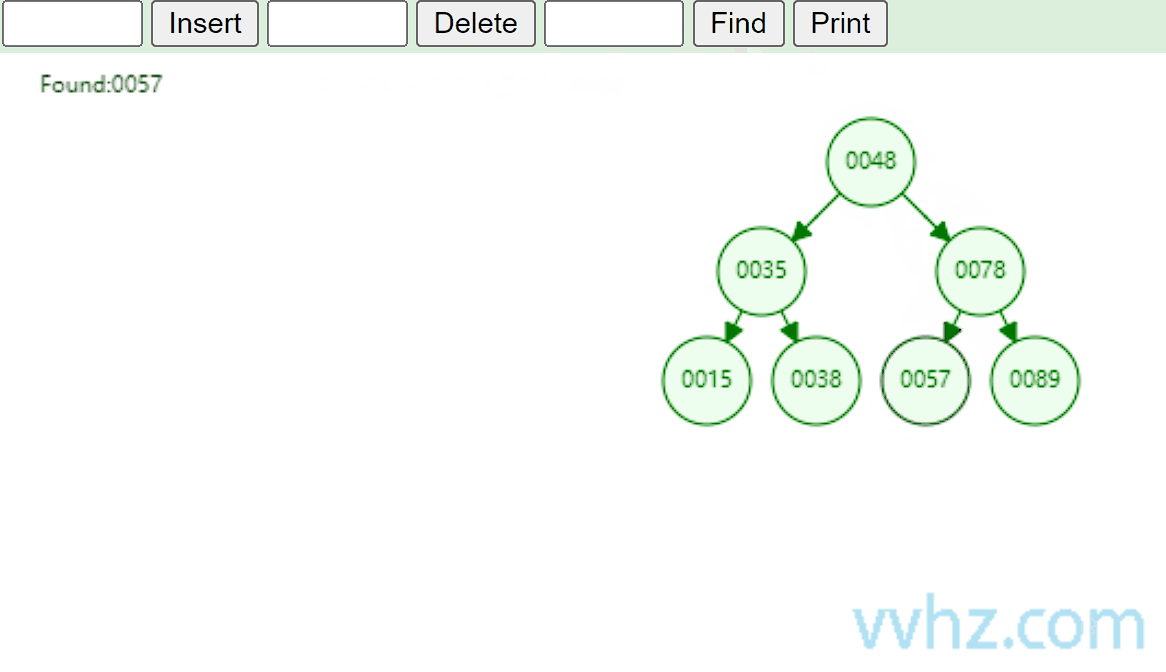
缺点:当二叉查找树退化为单链表时,比如,只有右子树的情况,如下图所示,此时查找效率为O(n)。

平衡二叉树(AVL 树):追求平衡
为了解决二叉查找树可能出现的不平衡问题,平衡二叉树(AVL 树)应运而生。AVL 树是一种高度平衡的二叉查找树,它通过旋转操作来保持树的平衡。AVL 树的每个节点都有一个平衡因子,平衡因子是该节点左子树高度与右子树高度的差值,其绝对值不超过 1。如果插入或删除节点导致某个节点的平衡因子绝对值大于 1,AVL 树就会通过左旋、右旋、左右旋、右左旋等操作来调整树的结构,使其恢复平衡。
比如,当在 AVL 树中插入一个节点后,导致某个节点的左子树高度比右子树高度大 2(平衡因子为 2),且插入节点在该节点左子树的左子树上,此时就需要进行右旋操作。右旋操作会将该节点的左子节点提升为新的根节点,原根节点变为新根节点的右子节点,新根节点原来的右子节点变为原根节点的左子节点,从而使树恢复平衡。
由于 AVL 树始终保持平衡,其查询时间复杂度稳定在 O (logN),这使得它在数据查找方面表现出色。但当数据量非常大时,AVL 树也存在一些不足。虽然它能保证树的平衡,但随着数据量的增加,树的层级仍然会逐渐变高。因为 AVL 树本质上还是二叉树,每个节点最多只有两个子节点,在大数据量下,为了存储这些数据,树不得不增加层级。而树的层级越高,从根节点到叶子节点的路径就越长,查询时需要访问的节点数量也就越多,这会增加磁盘 I/O 次数(如果数据存储在磁盘上),从而影响查询效率。
B 树:多路平衡的改进
B 树是一种多路平衡查找树,它在 AVL 树的基础上进行了改进,通过增加节点的分支数,来减少树的层级,提高查询效率,非常适合在磁盘等外存设备上存储和查找数据。
B 树的节点结构与二叉树有很大不同。一个 m 阶的 B 树,每个非叶子节点最多可以包含 m - 1 个关键字和 m 个指针,最少包含⌈m/2⌉ - 1 个关键字和⌈m/2⌉个指针 。关键字按照从小到大的顺序排列,并且第 i 个关键字和第 i + 1 个关键字之间的指针指向的子树中,所有节点的关键字值都大于第 i 个关键字且小于第 i + 1 个关键字。例如,在一个 5 阶 B 树的节点中,可能包含 1 到 4 个关键字和 2 到 5 个指针。
B 树的数据存储方式也有其特点,在 B 树中,数据并非仅存在于叶子节点,而是允许非叶子节点与叶子节点共同存储数据 。每个节点除了存储数据,还包含指向子节点的指针。
在插入操作中,如果插入一个关键字后导致某个节点的关键字数量超过 m - 1,节点就会进行分裂。分裂时,将节点中间位置的关键字提升到父节点中,原节点被分成两个新节点,分别包含原来节点中一半左右的关键字和指针。删除操作相对复杂一些,如果删除关键字后导致某个节点的关键字数量小于⌈m/2⌉ - 1,就需要从兄弟节点借关键字或者与兄弟节点合并来保持树的结构和性质。例如,在一个节点中删除关键字后,关键字数量不足,若其兄弟节点有多余的关键字,就从兄弟节点借一个关键字过来;若兄弟节点也没有多余关键字,则与兄弟节点合并成一个节点。通过这些插入和删除操作时的调整策略,B 树能够始终保持平衡,确保高效的查询性能。
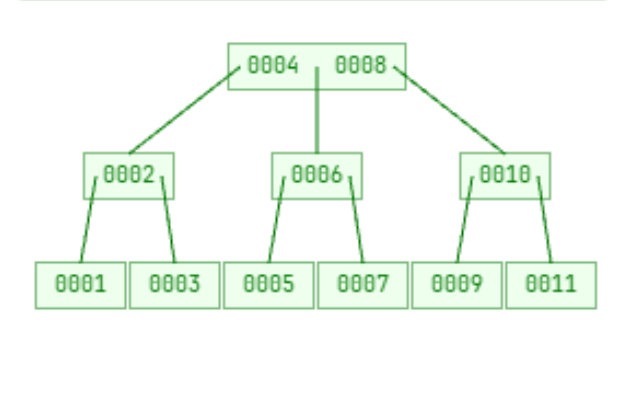
下面是一个3阶B树插入1-11这些元素后的结构
B + 树:MySQL 的 “宠儿”
B + 树是 B 树的一种变体,在 MySQL 数据库中,B + 树是最常用的索引数据结构,深受数据库开发者的青睐。
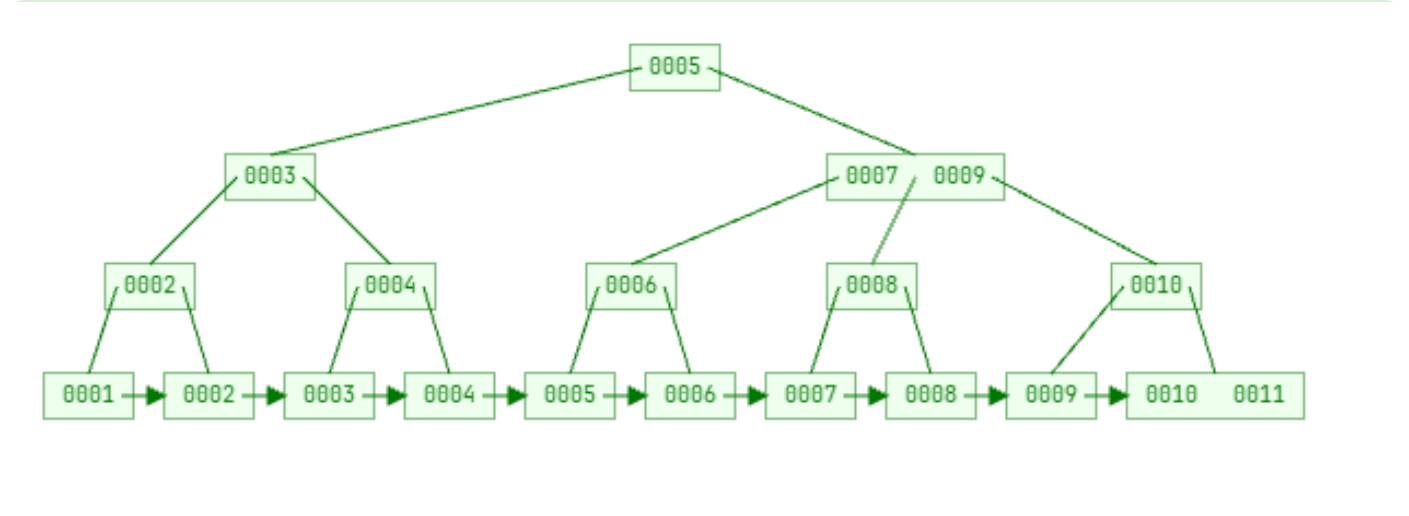
B + 树与 B 树存在一些关键区别。在 B + 树中,只有叶子节点存储数据,非叶子节点仅存储索引信息,这使得非叶子节点可以存储更多的索引项,进一步降低了树的高度,提高了查询效率。例如,在一个存储大量用户信息的数据库表中,使用 B + 树索引时,非叶子节点可以快速定位到包含目标用户数据的叶子节点所在位置,而无需像 B 树那样在非叶子节点中也存储部分数据。
B + 树的叶子节点通过双向链表连接,这是 B + 树的一个重要特性,也是它在范围查询和排序操作上表现出色的原因。当进行范围查询时,比如查询年龄在 20 到 30 岁之间的用户,只需要找到年龄为 20 的叶子节点,然后通过链表依次遍历后续节点,直到找到年龄大于 30 的节点为止,这个过程非常高效,避免了像其他数据结构那样需要多次回溯查找的问题。在排序操作中,由于叶子节点是有序的,并且通过链表连接,所以可以直接按照链表顺序进行排序,无需额外的排序算法,大大提高了排序效率。
在实际的 MySQL 数据库应用中,B + 树的这些特性得到了充分的发挥。无论是处理大量的用户数据、订单数据还是其他各种类型的数据,B + 树都能提供高效的数据检索和操作能力,确保数据库系统的高性能和稳定性,这也是 MySQL 选择 B + 树作为主要索引数据结构的重要原因。
估算聚簇索引存储数量
当聚簇索引树高度为 3 层时最多能存储的数据量 :
前提条件
MySQL 默认数据页大小为 16KB(16 * 1024 = 16384 字节)。
主键为
int类型,占用 4 字节。表中有 10 个左右字段,假设每个字段平均占用 10 字节(这是一个大致估算,实际占用空间取决于字段类型),那么一条记录大约占用 10 * 10 = 100 字节,再加上 4 字节的主键,一条记录总共约占用 104 字节。
除了存储数据,每个节点还需要一些额外的开销来存储指针和节点头信息等,这里假设每个节点额外开销为 100 字节。
计算过程
1. 计算非叶子节点可存储的索引数量
非叶子节点主要存储索引和指向子节点的指针。指针通常占用 6 字节(不同版本可能略有差异)。
每个索引项包含一个 int 类型的主键(4 字节)和一个指向子节点的指针(6 字节),那么每个索引项占用 4 + 6 = 10 字节。
考虑到节点的额外开销 100 字节,每个非叶子节点可存储的索引数量为:
(16384−100)÷10≈1628(向下取整)
2. 计算第二层非叶子节点的数量
树的第一层是根节点,根节点可存储 1628 个索引,每个索引指向第二层的一个非叶子节点,所以第二层最多有 1628 个非叶子节点。
3. 计算第二层非叶子节点总共可存储的索引数量
每个第二层非叶子节点同样可存储 1628 个索引,那么第二层总共可存储的索引数量为:
1628×1628=2650384
4. 计算叶子节点可存储的数据记录数量
每个叶子节点存储的是完整的数据记录,每条记录约占用 104 字节,考虑到节点的额外开销 100 字节,每个叶子节点可存储的数据记录数量为:
(16384−100)÷104≈156(向下取整)
5. 计算树高度为 3 层时最多能存储的数据量
第二层的索引指向第三层的叶子节点,第二层有 2650384 个索引,也就意味着有 2650384 个叶子节点,每个叶子节点可存储 156 条数据记录,那么树高度为 3 层时最多能存储的数据量为:
2650384×156=413469904
总结
在上述假设条件下,聚簇索引树高度为 3 层时,最多大概能存储 4 亿多条数据。需要注意的是,这只是一个估算值,实际存储的数据量会受到字段类型、数据分布、页填充因子等多种因素的影响。
所以大多数情况下单表存储上千万数据只要做好查询优化是没有任何问题的。
哈希索引:特殊场景的利器
哈希索引的原理与特点
哈希索引是一种独特的索引类型,它的工作原理基于哈希函数。哈希函数就像是一个神奇的 “翻译器”,能将索引键值转换为一个固定长度的哈希值,这个哈希值就像是数据的 “门牌号”,指向哈希表中特定的存储位置(也称为桶)。通过这种方式,哈希索引实现了快速的数据查找,其查找时间复杂度通常能达到惊人的 O (1) ,这意味着无论数据量有多大,理论上都能在常数时间内找到目标数据,就像你在一个拥有无数房间的大楼里,通过门牌号能瞬间找到你要去的房间一样。
例如,在一个用户信息数据库表中,假设我们使用用户 ID 作为哈希索引的键值。当我们要查询 ID 为 1001 的用户信息时,哈希函数会将 1001 这个键值转换为一个哈希值,比如 5678 ,然后根据这个哈希值直接定位到哈希表中对应的桶,在这个桶中就能快速找到 ID 为 1001 的用户信息,整个过程非常迅速,无需像其他索引结构那样进行多次比较和查找。
哈希索引在内存中的性能表现也十分出色。由于哈希表的结构相对简单,内存占用较少,在内存中进行查找操作时,哈希索引能够充分发挥其快速定位的优势,实现更高的查询速度。这使得哈希索引在内存数据库和缓存系统中得到了广泛的应用。
哈希索引的应用场景与局限性
哈希索引在某些特定场景下具有显著的优势。在缓存系统中,哈希索引能够快速定位缓存数据,减少 I/O 操作,提高系统性能。比如,在一个高并发的电商网站中,商品详情页面的数据通常会被缓存起来,使用哈希索引可以根据商品 ID 迅速从缓存中获取商品详情数据,大大减轻了数据库的压力,提高了页面的加载速度,为用户提供了更好的购物体验。在需要频繁进行等值查询的场景中,如查询用户 ID、订单编号等,哈希索引能够显著提高查询性能,快速返回查询结果。
然而,哈希索引也存在一些明显的局限性。它不支持范围查询和排序操作。由于哈希函数的特性,哈希索引指向的数据是无序的,无法按照索引键值的顺序进行存储,所以当我们需要查询某个范围内的数据,如查询年龄在 20 到 30 岁之间的用户,或者对数据进行排序时,哈希索引就无能为力了。在一个员工信息表中,如果要查询工资在 5000 元到 8000 元之间的员工,使用哈希索引就无法实现高效查询,只能通过全表扫描来获取结果,这会极大地降低查询效率。
哈希索引还存在哈希冲突的问题。当不同的键值经过哈希函数计算后得到相同的哈希值时,就会发生哈希冲突。虽然可以通过链地址法、开放地址法等方法来处理冲突,但当冲突较多时,会增加额外的存储和计算开销,导致性能下降。比如,在一个存储用户登录信息的表中,如果使用哈希索引,由于用户数量众多,可能会出现大量的哈希冲突,使得在查找用户登录信息时,需要遍历冲突链表中的多个节点,降低了查询速度。
实战应用:如何选择合适的索引数据结构
根据查询类型选择
在实际的数据库应用中,查询类型多种多样,而不同的查询类型对索引数据结构的要求也各不相同。
对于等值查询,如SELECT * FROM users WHERE id = 1001; ,哈希索引和 B + 树索引都能发挥作用。哈希索引凭借其基于哈希函数的快速定位特性,理论上能在 O (1) 的时间复杂度内找到目标数据,速度极快。但它的局限性在于只支持等值查询,并且存在哈希冲突的问题。B + 树索引虽然在等值查询的速度上可能稍逊于哈希索引,但它具有更广泛的适用性,不仅能处理等值查询,还能应对其他类型的查询。
当进行范围查询时,比如SELECT * FROM products WHERE price BETWEEN 50 AND 100; ,B + 树索引就展现出了它的强大优势。由于 B + 树的叶子节点是有序排列的,并且通过双向链表连接,数据库系统可以利用这些特性,快速定位到范围的起始和结束位置,然后沿着链表遍历,高效地获取范围内的数据。而哈希索引由于其数据的无序性,无法支持范围查询。
在排序查询中,例如SELECT * FROM employees ORDER BY salary; ,B + 树索引同样表现出色。因为 B + 树本身的结构保证了索引数据的有序性,数据库在执行排序操作时,可以直接利用 B + 树的有序特性,按照索引顺序读取数据,避免了额外的排序操作,大大提高了排序效率。而哈希索引不具备这种有序性,无法直接用于排序查询。
考虑数据量和数据分布
数据量的大小和数据分布情况是选择索引数据结构时需要重点考虑的因素。
当数据量较小时,各种索引数据结构的性能差异可能并不明显,因为此时全表扫描的成本相对较低,索引带来的性能提升可能不太显著。但随着数据量的不断增大,索引的作用就愈发重要。在大数据量的情况下,B + 树索引相较于其他一些结构具有明显的优势。由于 B + 树的非叶子节点仅存储索引信息,不存储实际数据,这使得每个节点可以存储更多的索引项,从而降低了树的高度。树的高度越低,从根节点到叶子节点的查找路径就越短,查询时需要访问的节点数量也就越少,这意味着可以减少磁盘 I/O 操作的次数。而磁盘 I/O 操作通常是数据库查询中最耗时的部分,减少磁盘 I/O 次数能极大地提高查询效率。
数据分布情况也会影响索引的选择。如果数据分布均匀,各种索引数据结构都能较好地发挥作用。但如果数据分布不均匀,存在大量重复值,那么索引的选择性就会降低,性能也会受到影响。在一个包含用户性别信息的表中,如果大部分用户的性别都是男性,只有极少数是女性,那么基于性别字段创建的索引在查询时的效率就会大打折扣,因为索引无法有效地过滤数据,可能导致大量的数据扫描。在这种情况下,可能需要考虑其他优化策略,如增加其他更具选择性的字段到索引中,或者采用其他更适合这种数据分布的索引结构。
实际案例分析
为了更直观地展示如何根据业务需求和数据特点选择合适的索引数据结构,我们来看一个实际的 MySQL 数据库应用案例。假设我们有一个电商网站的数据库,其中包含一个orders表,用于存储订单信息,表结构如下:
CREATE TABLE orders (
order_id INT AUTO_INCREMENT PRIMARY KEY,
customer_id INT,
order_date DATE,
total_amount DECIMAL(10, 2),
status VARCHAR(20)
);在这个表中,有以下几种常见的查询需求:
根据订单 ID 查询订单详情,如SELECT * FROM orders WHERE order_id = 12345; ,这是一个典型的等值查询。对于这种查询,我们可以选择在order_id字段上创建哈希索引或者 B + 树索引。由于订单 ID 通常是唯一的,哈希索引的快速查找特性可以在这里得到很好的发挥,能迅速定位到目标订单。但考虑到数据库中可能还存在其他查询需求,B + 树索引的通用性更强,所以在实际应用中,一般会选择 B + 树索引作为主键索引,既能满足等值查询的需求,又能适应其他查询场景。
查询某个时间段内的订单,例如SELECT * FROM orders WHERE order_date BETWEEN '2023-01-01' AND '2023-12-31'; ,这是一个范围查询。根据前面的分析,B + 树索引是最适合这种查询的。我们可以在order_date字段上创建 B + 树索引,利用其叶子节点的有序性和链表结构,快速定位到指定时间段内的订单数据。
按照订单金额对订单进行排序,如SELECT * FROM orders ORDER BY total_amount; ,B + 树索引同样能很好地支持这种排序查询。通过在total_amount字段上创建 B + 树索引,数据库可以直接按照索引顺序读取数据,高效地完成排序操作。
通过这个实际案例可以看出,在选择索引数据结构时,需要深入分析业务需求和数据特点,综合考虑各种因素,才能做出最适合的选择,从而优化数据库的查询性能,提升系统的整体运行效率 。
总结
在数据库的领域中,索引的数据结构种类繁多,每种都有其独特之处。二叉查找树以其简单的结构和二分查找特性,在数据量较小且分布均匀时能展现出一定的查找优势,但面对数据量增大和不平衡的情况,效率会大打折扣 。平衡二叉树(AVL 树)通过严格的平衡条件和旋转操作,保持了树的平衡,稳定了查询性能,但在大数据量下,树的层级仍然会成为查询效率的制约因素。
B 树通过增加节点分支数,有效减少了树的层级,提高了磁盘 I/O 效率,非常适合在磁盘存储中使用。而 B + 树作为 B 树的优化版本,更是 MySQL 数据库的 “宠儿”。它将数据全部存储在叶子节点,非叶子节点仅用于索引,进一步降低了树的高度,并且叶子节点通过双向链表连接,使得范围查询和排序操作变得高效。哈希索引则凭借其基于哈希函数的快速定位能力,在等值查询和内存性能方面表现出色,但在范围查询和排序上存在明显短板。
